Fachgebiet Stochastic Finance
Die Ziele im Bereich der Stochastic Finance sind die Beschreibung und Analyse von Aktien-, Zins- und Kreditmärkten. Dies umfasst insbesondere die Bewertung von Finanzprodukten, die auf obigen Märkten angeboten und nachgefragt werden, die quantitative Erfassung und Steuerung von Risiken, die mit dem Handel der Finanzprodukte einhergehen und die Analyse von Ertrags-Risiko-Strukturen.
Grundlegend für alle genannten Ziele ist die Betrachtung der zukünftigen Preisentwicklung von Finanzinstrumenten (z.B. Aktien) an den Märkten. Um die Preisentwicklung adäquat abzubilden, sollten die zeitliche Dynamik und die Unsicherheit der Information berücksichtigt werden. Zu diesem Zweck werden in Finanzmarktmodellen spezielle stochastische Prozesse herangezogen, die jeweils mit einer zugrundeliegenden Verteilung korrespondieren und die z.B. danach unterschieden werden können, ob sie stetig sind oder Sprünge aufweisen oder etwa ein Mean-Reverting-Verhalten widergeben. Je nachdem, wie viele stochastische Einflussgrößen in ein Modell eingehen, spricht man von Ein- oder Mehrfaktormodellen.
So kann man beispielsweise die Entwicklung eines Aktienindices wie dem S&P 500 über eine Zeitspanne von mehreren Jahren hinweg simulieren und das Ergebnis grafisch darstellen.
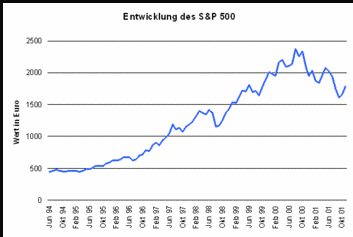
Der Simulation liegt typischerweise ein Modell zugrunde. Dieses kann z.B. mittels einer stochastischen Differentialgleichung definiert werden.
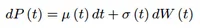
Im Anschluss an die Modellierungsphase, in welcher man den strukturellen Ansatz festlegt, bestimmt man mittels statistischer Verfahren (Maximum Likelihood, Kalman-Filter, LSE-Methode, ...) anhand von Marktdaten die freien Parameter im Modell (Phase des Parameterfittings). Die implizite Anpassung erfolgt über die Betrachtung gegenwärtiger Marktpreise der modellierten Assets, wohingegen die historische Anpassung auf Daten der Vergangenheit beruht.
Das angepasste Modell kann dann seiner Anwendung zugeführt werden, z.B. der Bewertung von Derivaten, die als Underlying dasjenige Asset aufweisen, dessen Preis im Modell abgebildet wird. Das Payoff-Profil eines Derivates kann dann in einem Payoff Diagramm abgebildet werden.
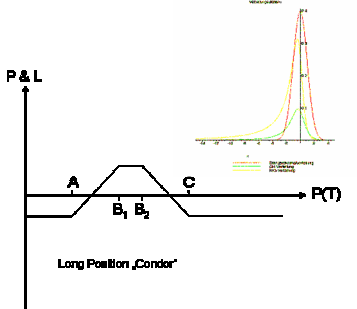
Des Weiteren ist die Ableitung modellkonformer Risikokennzahlen denkbar, die als Grundlage für die Kontrolle und Steuerung respektive Reduktion der Marktrisiken (Kreditrisiken) dient. Bei der Bewertung von Finanzderivaten ist es häufig der Fall, dass keine geschlossene Preisformel mehr angegeben werden kann. Hier setzt dann die Computational Finance an, die mittels numerischer Methoden und Simulationstechniken Näherungslösungen eruiert. Sowohl private als auch institutionelle Anleger verfolgen im Rahmen eines Risikomanagements, das sich der Risikoanalyse anschließt, das Ziel, ein Portfolio von marktgängigen Assets zusammenzustellen, das ihren persönlichen Präferenzen hinsichtlich Risiko und Ertrag am „nächsten“ kommt. Mit dieser Problemstellung setzt sich im Wesentlichen die Financial Optimization auseinander.
Aktuelle Themenstellungen am Lehrstuhl für Finanzmathematik im Bereich Stochastic Finance sind u.a.
- Entwicklung stochastischer Volatilitätsmodelle
- Risikoanalyse in Lévy-Märkten
- Portfoliooptimierung in unvollständigen Märkten
- hybride Kreditrisikomodelle
- Kreditrisikomodelle mit unvollständiger Information