Fachgebiet Financial Optimization

Bereits 1952 legte Harry Markowitz den Grundstein für die sog. Mean-Variance-Analyse. Er beurteilte Aktien bzw. Wertpapiere nicht nur anhand ihrer Renditen, sondern bezog auch die Varianzen und Kovarianzen bei der Zusammenstellung von Portfolios mit ein. Dieser Ansatz führt zu dem grundlegenden einstufigen Optimierungsproblem, welches den Portfolio-Return unter Einhaltung einer gegebenen Risikoschranke maximiert. In dieser Formulierung werden also nur die ersten beiden Momente einer Verteilung betrachtet, der Return wird durch den Mittelwert beschrieben und das Risiko durch die Varianz.

Die mathematische Formulierung der Problemstellung lautet wie folgt.

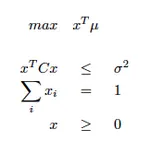
Löst man dieses Optimierungsproblem für verschiedene Risikoschranken (σ^2), so erhält man die Menge aller effizienten Portfolios, die hier im μ-σ-Diagramm dargestellt ist.

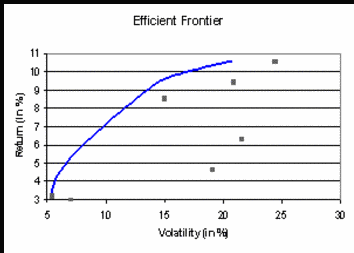
In der Praxis sind oft noch weitere Nebenbedingungen gefordert, beispielsweise

die Zulassung von Leerverkäufen,
zusätzliche Gewichtsbeschränkungen in Sektoren, Ländern, Einzeltiteln,
die Beschränkung der Anzahl der Titel im Portfolio,
die Berücksichtigung von Transaktionskosten, Cash Flows, Liabilities

Ausgehend von obigem Programm lassen sich auch Modelle für andere Problemstellungen formulieren wie z.B. die Portfolio-Optimierung relativ zu einer Benchmark oder die Minimierung des Tracking-Errors.

Dieses einfache Modell von Markowitz hat allerdings auch Nachteile. Es ist ein einstufiges Optimierungsproblem (Zwei-Zeitpunkt-Betrachtung), was in der Praxis oft nicht ausreichend ist: so ist man z.B. an optimalen Anlagestrategien über die Zeit interessiert, d.h. nicht nur die aktuelle Allokation ist relevant, sondern auch die potentiellen Portfolio-Umstrukturierungen im Laufe der Zeit. Diese Problemstellung führt zur mehrstufigen dynamischen Optimierung.

Des Weiteren reagieren die Ergebnisse der Markowitz-Optimierung sehr sensitiv auf die Inputdaten, weshalb robustere Lösungen und Lösungsverfahren gesucht werden. Auch hierfür gibt es verschiedene Ansätze.

Das Markowitz-Modell zieht nur die ersten beiden Momente einer Verteilung in Betracht. Unter der Annahme, dass die Renditen der in der Optimierung betrachteten Wertpapiere einer Normalverteilung folgen, reichen die ersten beiden Momente aus, um die Verteilung zu charakterisieren.

Allerdings werden in der Praxis nicht nur Wertpapiere betrachtet, für die eine solche Normalverteilungsannahme zulässig ist, sondern es können auch Portfolios mit deutlich asymmetrischen Verteilungen entstehen, z.B. durch die Hinzunahme von Optionen. Dann reichen Erwartungswert und Varianz nicht mehr aus, und eine Optimierung basierend auf diesen ersten beiden Momenten ist nicht adäquat.

Die Varianz ist ein Maß für die Streuung um den Erwartungswert – in beide Richtungen. Bei der Risikomessung in der Finanzwirtschaft ist vor allem aber die Unterschreitung einer gegebenen Benchmark wichtig, denn nur Verluste stellen ein wirkliches Risiko dar. Ein weiteres Risikomaß sind daher z.B. Shortfall-Bedingungen, die in die Optimierung mit eingehen. Dies führt zur stochastischen Optimierung, indem beispielsweise gefordert wird, dass die Wahrscheinlichkeit, Verluste zu machen, nicht größer ist als α% oder dass der erwartete Verlust einen bestimmten Vermögensbetrag nicht übersteigt.

Bei komplizierteren Portfolio-Strukturen oder Verteilungen oder bei Betrachtung von Anlagestrategien über die Zeit lassen sich Return und Risiko oft nicht mehr als geschlossene Formel angeben. Hier kann man z.B. Szenarien als Grundlage der Optimierung betrachten.

Mit Hilfe von Modellen für die verschiedenen Märkte werden die Assets bzw. Asset Klassen über die Zeit hinweg simuliert. Basierend auf diesen Szenariopfaden werden verschiedene Portfolios oder Anlagestrategien berechnet, aus welchen die „optimale“ Strategie ausgewählt werden kann.

Die Szenario-Simulation lässt sich wie folgt veranschaulichen.

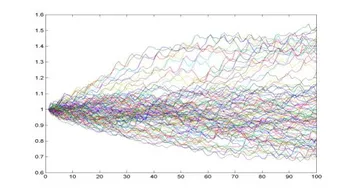
Aktuelle Themenstellungen am Lehrstuhl für Finanzmathematik im Bereich der Financial Optimization sind u.a.

Robustifizierung der Lösungen von Optimierungsproblemen durch verschiedene Ansätze
Einbindung von Expertenprognosen in die Optimierung
Anwendung genetischer Verfahren zur Lösung von Portfolio-Optimierungs-Problemen
Optimierung von Anlagestrategien