Fachgebiet Computational Finance
Die Finanzmathematik hat viele Modelle hervorgebracht: von amerikanischen Optionen bis zu Zinsstrukturmodellen. Im praktischen Einsatz werden aber höchst selten die Formeln direkt gebraucht. Ein Optionsscheinhändler benötigt Zahlen, um seine Modelle zu "füttern" und sein Ergebnis ist wiederum eine Zahl: der Preis.
Man begegnet mehreren Herausforderungen dabei. Auf der einen Seite müssen die Eingangsdaten geschätzt werden. Dieses Problem gehört zur Ökonometrie. Auf der anderen Seite müssen die oft abstrakt formulierten Modelle auf dem Computer umgesetzt werden. Dabei treten Probleme aus der Informatik, der Optimierung und der Numerik auf. Diese Probleme werden in der Computational Finance betrachtet. Zusätzlich werden die Modelle erweitert, sodass effiziente und praxisnahe Lösungen entstehen.
Das faire Bewerten einer europäischen Call Option beschäftigt die Händler schon seit langer Zeit. Schon im 17. Jahrhundert wurden ähnliche Optionen gehandelt. Doch erst 1973 gelang der Durchbruch zu einer konsistenten Theorie. Heute kennt man viele verschiedene Arten, diesen fairen Preis zu berechnen. Wir stellen Ihnen im Folgenden die wichtigsten Berechnungsarten vor.
1. Einsetzen in die Black-Scholes-Merton Formel (geschlossene Lösung) [1]
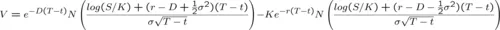
2. Anwenden des Cox-Ross-Rubenstein Binomialbaums [2]
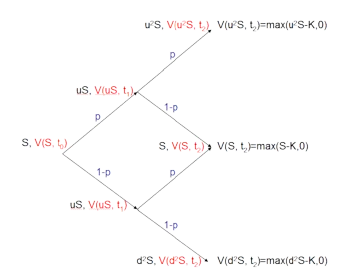
3. Risikoneutrales Simulieren (Monte Carlo) nach Boyle [3]
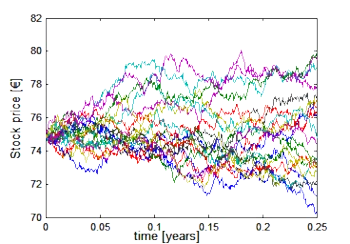
4. Lösen der Black-Scholes Gleichung (PDE) durch Diskretisierung [4]
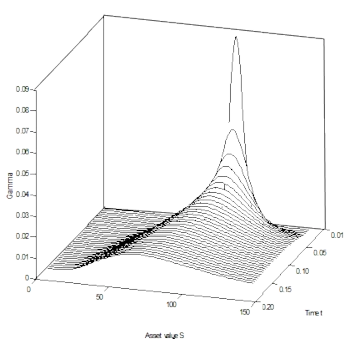
Diese Lösungsmöglichkeiten haben verschiedene Vor- und Nachteile. Während sich die geschlossene Lösung einfach implementieren lässt, ist der Binomialbaum besonders einfach zu verstehen. Die Monte Carlo Simulationen und PDE Methoden sind sehr gut zu verallgemeinern und auf realistischere Szenarios anwendbar. Welche Methode eingesetzt wird, hängt stark von dem konkreten Problem ab und den Rahmenbedingen wie z.B. Speicherplatz und verfügbare Rechenzeit.
Aktuelle Themenstellungen am Lehrstuhl für Finanzmathematik im Bereich der Computational Finance sind u.a.
- pfadabhängige Optionen (Preisen und Hedgen von Asian und Parisian Options)
- komplexe Vereinbarungen bei Wandelanleihen (moving windows, notice periods)
- Optionen auf makroökonomische Kenngrößen (Makroderivate)
- Kombinationen von Monte Carlo Simulation und PDE Lösung
Literatur:
[1] Fischer Black and Myron Scholes: "The pricing of options and corporate liabilities", Journal of Political Economy, 1973, No. 81, p. 637-659
[2] John Cox, Stephen Ross and Mark Rubenstein: "Option pricing: A Simplifyed Approach", Journal of Financial Economics, 1979, No. 7, p. 229-263
[3] Phelim P. Boyle: "Options: A Monte Carlo Approach", Journal of Financial Economics, 1977, No. 4 (3), p. 323-338
[4] Paul Wilmott: "Paul Wilmott on Quantitative Finance", John Wiley & Sons Ltd., 2000, West Sussex, England