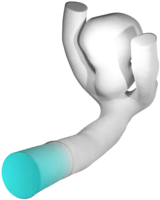- 3Numerical simulation of individual coil placement -- A proof-of-concept study for the prediction of recurrence after aneurysm coiling. 2024 mehr… BibTeX
- 2Directional flow in perivascular networks: Mixed finite elements for reduced-dimensional models on graphs. 2023 mehr… BibTeX
- 1A 1D-0D-3D coupled model for simulating blood flow and transport processes in breast tissue. International Journal for Numerical Methods in Biomedical Engineering 38 (7), 2022 mehr… BibTeX Volltext ( DOI ) Volltext (mediaTUM)
Numerical simulations for the treatment of cerebral aneurysms (SPP2311)
Within the SPP program 2311 of the Deutsche Forschungsgemeinschaft, organized at the university of Stuttgart, our chair is part of the project "Multi-scale algorithms and simulation for the patient-specific optimization of endovascular interventions in cerebral aneurysms" in cooperation with the group of Prof. Alexander Popp (Universität der Bundeswehr München) and Prof. Jan Kirschke (Neuro-Kopf-Zentrum Klinikum rechts der Isar, TUM).
Within the project we develop numerical simulations of the treatment of cerebral aneurysms such as via endovascular coiling. We therefore consider mathematical models, methods and tools from computational fluid and haemodynamics, porous media flow and homogenization, over mechanical & surrogate models up to high-performance computing aspects with e.g. the lattice-Boltzmann method. Via these simulations our goal is to be able to assess the rupture risk of aneurysms for actual clinical and patient specific cases as well as to test - and eventually even optimize - the success of treatment methods in silico.
Links to program and further project webpages:
- SPP2311: Webpage at University of Stuttgart
- DFG-Program: Program-webpage of the DFG
- Project-subpage @SPP2311: Project-webpage at University of Stuttgart
Project Overview
The following blocks will give an overview over the challenges, methods and current results of our work on the project. Details about each of them can be found in the original publications listed at the bottom of this page.
Patient specific geometry acquisition
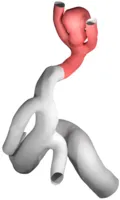
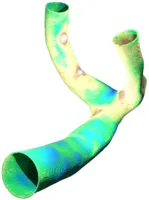
Every human is different. Not just on the character and outside, but also literally on the inside. Hence, the geometry of blood-vessels as well as aneurysms formed on their surface differs from case to case with respect to size, shape and position, e.g. whether it is on the side of a straight vessel or right at a bifurcation point. These different dimensions of aneurysm classification are extremely important when it comes to the choice of the concrete medical treatment device to be used. Hence, for a detailed in silico analysis in advance of any surgigcal intervention, it is also of importance to have highly-resolved, patient-specific (vessel- and aneurysm)-geometries at ones disposal, which can be used as computational domains in numerical simulation codes. The usual pipeline we are following to obtain such geometries is as follows:
- Segmentation of medical MRI, CT, general angiography imaging data to obtain a 3D-model of the vascular-tree of the neighborhood adjacent to the aneurysm.
- Preprocessing of the vessel geometry by means of mesh quality and scale, truncation to the desired region of interest as well as the addition of tube-like flow-extensions in order to obtain an already developed flow within the actual vessel geometry.
- Measuring of the aneurysm e.g. by computing area and volume, or - for the adjacent vessel - computation of a center-line and vessel radius information for later stent-placement.
- Meshing of the computational domain to fit to the solver requirements. Depending on the numerical solver to be used, a volumetric mesh consisting out of tetraeders or hexaeders (in LBM even cubes) is computed.
- Normal computation is something non-trivial in e.g. LBM-related meshes using a staircase approximation of curved surfaces. However, normals are important for later evaluation of quantities of interest such as wall-shear-stress
Lattice-Boltzmann driven haemodynamics
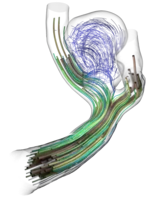
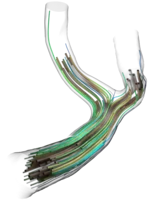
For the haemodynamical (=blood flow) simulations within this project we employ the Lattice-Boltzmann method (LBM) implemented in the high-performance software framework waLBerla. In contrast to classical numerical schemes such as Finite Differences (FD), Finite Elements (FE) or Finite Volumes (FV), LBM are not based on the macroscopic equations such as Navier-Stokes-equation directly, but rather on a mesoscopic, particle-density level. The method relies on gas-dynamical concepts such as equilibrium distributions and particle collisions from statistical mechanics that ``on average'' again yield solutions to the classical fluid mechanical equations. A few aspects that make computational haemodynamics interesting:
- Pulsation of bloodflow in the rhythm of heart-beats with changing velocity amplitudes and pressure levels makes such flow-patterns non-stationary and highly oscillative. A dimensionally reduced model for the propagation of these oscillations through the human vessel-system, from the large arteries up to the capillaries in specific tissue is analyzed in our publication [1] and its output then used as boundary conditions for our fully resolved 3D simulations
- Non-Newtonian nature of bloodflow makes the viscosity of blood non-constant in comparison to e.g. water, where it is just a given material parameter. Non-Newtonian flow models need to update viscosity from timestep to timestep leading to different, in low shear-rate regimes even plug-like, flow behavior
- Blood coagulation and clotting which takes place e.g. at injuries of blood-vessels or certain shear-rate areas (in implanted treatment-devices), is a highly complex bio-chemical process, which however is important to consider and understand w.r.t. to the desired treatment and occlusion of aneurysms or the modeling of arterial stenosis.
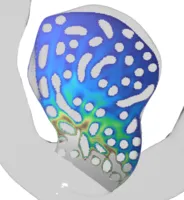
Modelling endovascular treatment devices
Except from a surgery such as clipping of aneurysms, endovascular techniques are a growing technology. Thereby treatment devices such as stents, web-devices or coils are inserted and properly placed via a catheter into the (vicinity of the) aneurysm. The different devices follow different strategies, but they have in common the goal to suppress further blood-circulation within the sack of the aneurysm to reduce the wall wear-out due to increased wall-shear-stress and oscillating blood pressure. It is our goal to model different kinds of these devices either mechanically or geometrically in order to have realistic device-shapes available to be inserted - like obstacles - into our haemodynamical simulations and to analyze the effect they have on the flow-pattern and the aforementioned goal to eventually fully occlude the aneuryms from it.
- Coils are very fine micro-wires protruded into the aneurysm, coiling up therein and hence filling it out volumetrically. Even though being extremely thin, such coils bear a complicated helical micro-structure making them extremely soft to avoid piercing the aneurysm during the insertion procedure. With details being up to individual manufacturer's secrets, certain framing-coils are also build with an inherent ``goal shape'' they try to attain once protruded from the catheter to stabilize the aneurysm's dome with a basket-like structure before further, and more softer, filling coils are inserted. We model and simulate coils as one-dimensionally connected mass-spring systems, where the springs model different mechanical effects such as stretching, bending or torsion. Together with some contact modelling avoiding self- and surface-penetration these comparably simple models already deliver quite realistic coil shapes.
- Web-Devices are also inserted into the aneurysm's sack via a catheter, however they more correspond to a two-dimensional thin manifold structure lining the surface of the aneurysm than a one-dimensional coiling-wire. Instead of filling out the aneurysm volumetrically as the coil, they can again be compared with a very narrow-woven basket structure shielding the aneurysm from blood-flow in between the wires.
- Stents / Flow diverters follow a similar idea as web-devices, however, they are not placed inside the aneurysm but actually before the aneurysm within the adjacent vessel in order to guide the blood-stream across, but not inside the aneurysm. Often they are also used in combination with e.g. a coil that is inserted into the aneurysm, where the stent-craft prevents the coil from falling out of the aneurysm and hence to keep it in place.
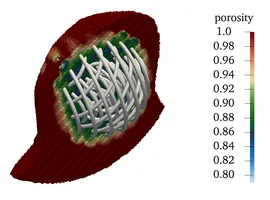
A porous medium surrogate model via homogenization
All the medical devices introduced before have two things in common: First, they exhibit very fine-grained (wire)-structures, which - if one wishes to fully resolve them - pose considerable computational requirements. Second, however, we are usually not even interested in the exact microscopic flow pattern of blood around each individual wire of e.g. a coil, but rather the general flow-rate within the aneurysm after treatment, i.e. we would like to look at the devices from "further appart" or with a say a bit "blurry vision". In the language of mathematical modelling we are searching for a surrogate model, that is simpler (less efford) but still yields comparable results. Taking for example a fully inserted coil we proceed as follows:
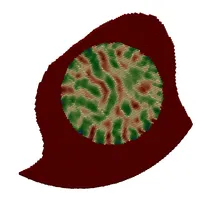
- Porous Medium interpretation of the coil as an (in)homogeneous porosity and permeability field instead of the fully resolved wires. Hence, instead of placing the device as a fully resolved obstacle, we place a body force by means of a Darcy and a Forchheimer term on the right hand side of the fluid-mechanical (Navier-Stokes) equation, yielding a model for porous medium flow. We can then remove the actual device but still obtain the flow-hindering effect of it due to the presence of the porous medium.
- Homogenization procedures allow us to actually derive a sensible porosity and, e.g. via suitable Kozeny-Carman relations, permeability field from a given coil structure by locally averaging the pore-space (in between coiling-wire-loops) in relation to the total volume within the aneurysm sack. These procedures, in combination with directivity information from the device-models also allow us to derive an orthotropic permeability tensor, hence also observing anisotropic porous medium behavior.