Lattice Boltzmann methods
In contrast to traditional computational fluid dynamics (CFD) approaches based on the conservation of macroscopic quantities like mass, momentum, and energy, the Lattice Boltzmann method (LBM) models the fluid by the kinetics of discrete particles that propagate (streaming step) and collide (relaxation step) on a discrete lattice mesh. Due to its particular nature, LBM has several advantages, such as dealing with complex boundaries, incorporating microscopic interactions, and parallelization of the algorithm.
Problem setting and motivation
- Due to its flexibility concerning complex geometries, Lattice Boltzmann methods can be used for the simulation of porous media or micro-fluidic devices on a very fine scale.
- Also interface problems between a free-flow and porous media regimes with suitable coupling conditions can be treated in an elegant way using the Lattice-Boltzmann method.
- Analysis of different collision operators, lattice-stencils and boundary conditions for various problem settings and flow regimes over a wide range of Raynolds numbers.
- Multiphase and turbulent flow simulations at high Reynolds numbers.
- Highly parallel and efficient implementation of the Lattice-Boltzmann schemes.
A selection of results
Porous media simulation
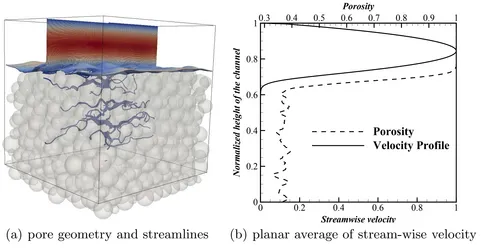
Instead of a homogenized continuum approach automatic particle generation on the pore scale can be employed to model the porous medium. The Lattice Boltzmann method is then used to simulate the fluid flow between the solid particles. The transition from porous medium to free flow can be seen in the following picture. Also streamlines visualizing the flow in the porous medium are depicted.

Two phase fluid
Simulation of the instability induced mixing process of a two component fluid simulated using the Lattice Boltzmann method.

