(Keine Dokumente in dieser Ansicht)
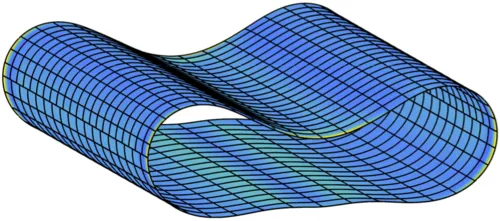
Isogeometric mortar methods
In collaboration with several engineering groups, we worked on more computationally efficient and more flexible weak coupling strategies including cross-point modifications, higher order coupling and hybrid versions.
Problem setting and motivation
Isogeometric analysis is a modern paradigm in numerical analysis, particularly in solid mechanics. The same set of functions are used to precisely describe the geometry and solution of the PDE, e.g. the displacement of a solid body according to the equations of elasticity.Complex geometries usually cannot be described as a single spline geometry, but as a multi-patch geometry. Here weak patch-coupling is an important feature in practical applications as is retains the flexibility within each patch.
Results
We investigate both the mathematical properties as well as the practical applicability. We have shown inf-sup stability of several Lagrange multiplier spaces and the resulting optimal convergence rates. Besides standard Lagrange multipliers, also the use of biorthogonal basis functions is investigated, where the coupling condition can locally be eliminated and the indefinite saddle point problem is reduced to a positive definite equation system. Complex applications include higher order PDEs and applications in vibro-acoustics.Pressurized hollow sphere of a non-linear Neo-Hooke material coupled with biorthogonal Lagrange multipliers:
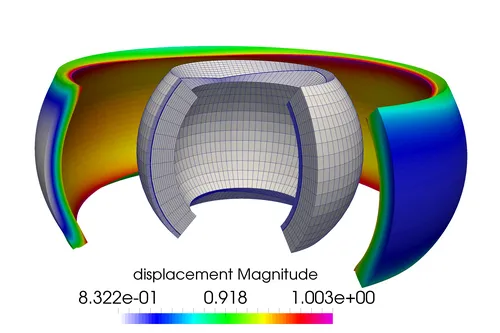
Pinched cylinder with a weak G1 coupling:
