Acoustic wave phenomena
Research in the field of acoustic wave phenomena at our Chair includes a range of topics, from the analysis of (non)linear acoustic wave models, coupling strategies of acoustics to other physical fields such as elasticity or thermodynamics, and the development of accurate absorbing boundary conditions to shape optimization of acoustic focusing devices.
Problem setting and motivation
Accurate simulation of ultrasound offers a path to a better quality of numerous procedures in industry and medicine, from non-destructive detection of material damages to ultrasound imaging and non-invasive treatments of medical disorders. The goal of our work is to mathematically analyze, efficiently simulate, and in the end optimize sound waves.
Nonlinear acoustics
Propagation of high-intensity ultrasound through thermoviscous fluids can be modeled by Westervelt's equation $$\Large \psi_{tt}-c^2\Delta\psi-b\Delta\psi_t = 2k\psi_t\psi_{tt}.$$
Westervelt's equation is a strongly damped quasilinear wave equation that provides challenges both in analysis and simulation.
Self-adaptive absorbing boundary conditions
In numerical simulations of ultraounds, the large physical space often has to be truncated. To accurately simulate ultrasound, we have to avoid spurious reflections of the wave at the boundary of the truncated domain. Absorbing boundary conditions provide a simple, yet effective way of dealing with unwanted reflections. Our self-adaptive method locally computes the incidence angle and updates the absorbing conditions on the fly, basing the local angle computation on the gradient of the wave field.
Efficient focusing of sound waves based on shape optimization
Focusing in ultrasound applications is achieved geometrically, with lenses or spherical focusing arrays of piezoelectric transducers. Such setups can naturally benefit from shape optimization: we can find the shape of the lens or the transducer surface which results in a desired pressure distribution around the focal point.
A selection of results
A selection of results
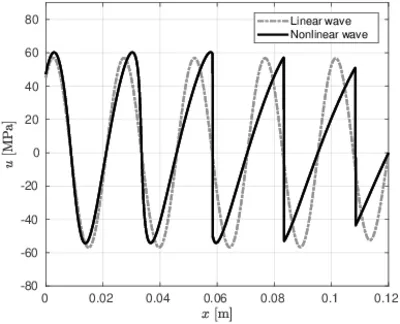
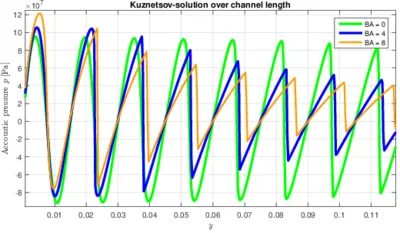
The following picture (left) shows a direct comparison between a classical/linear wave propagation and a nonlinear one (Westervelt's equation). In the nonlinear case steepening of the wave front is happening until a shock is reached, causing the wave to lose energy and hence decrease in amplitude. The picture on the right shows the influence of the parameter of nonlinearity B/A on the solution of Kuznetsov's equation. The higher B/A gets, the more pronounced the nonlinear nature of the equation becomes.
The following picture shows a 2D simulation of Blackstock's equation in a transducer/focusing geometry. Starting from an arc shaped part of the boundary the wave travels towards a common focal point increasing in amplitude and developing a sharp shock front. After the focal point the wave spreads into the domain behind again decreasing in amplitude. Such behaviour is used for the treatment of for example kidney stones via extra corporeal shockwave lithotripsie, where large amounts of pressure are exerted precisely onto a kidney stone in order to break it into smaller pieces, while surrounding tissue must not be harmed by high pressure amplitudes.

Shape Optimization for nonlinear ultrasound focusing
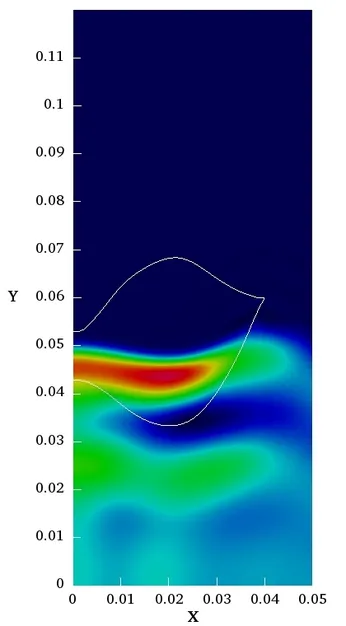
Similar to the curved transducer geometry from above, focusing of an ultra-sound wave can be reached by sending the wave through an acoustic focusing lens. Such behaviour can be observed in the next picture where the cross-section of a (nonlinear) wave can be seen developing steepening as well as being focused towards the axis of symmetry:
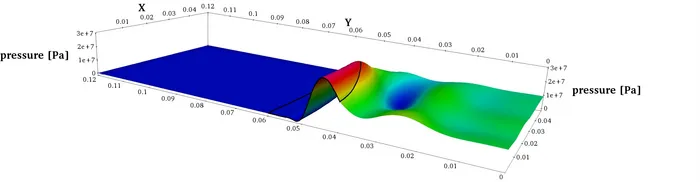
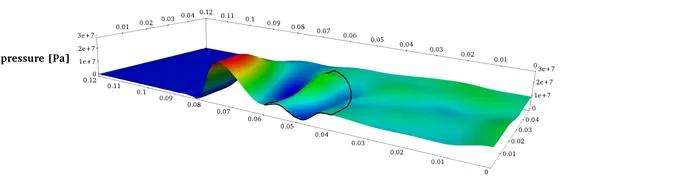
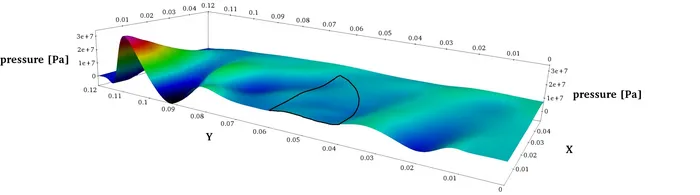
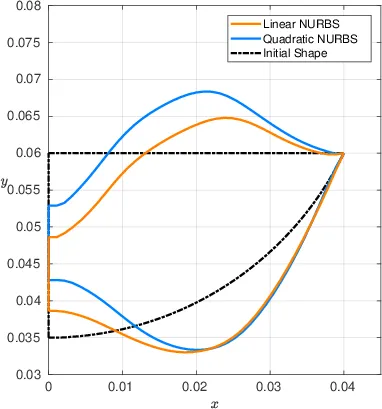
The shape of the acoustic focusing lens plays a crucial role in trying to achieve precise focusing. Different shapes might exhibit different focusing properties. Finding an optimal shape is subject to our work in shape optimization. The following picture shows optimization results using linear and quadratic NURBS (isogeometric analysis framework) together with an initial configuration.
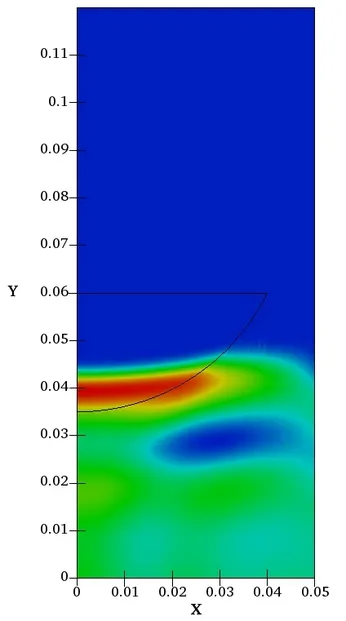
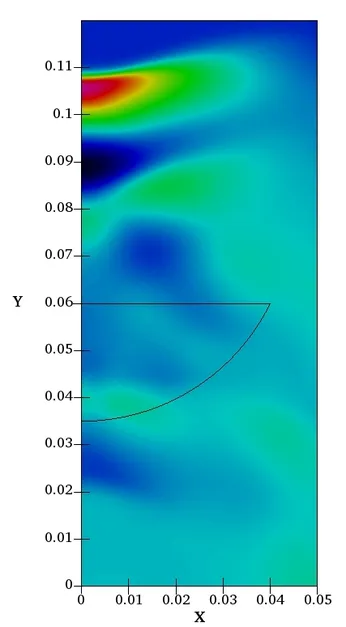
The effect of the optimized lens can be observed in the following comparison of acoustic pressure distributions between the initial (left) and optimized (right) shape
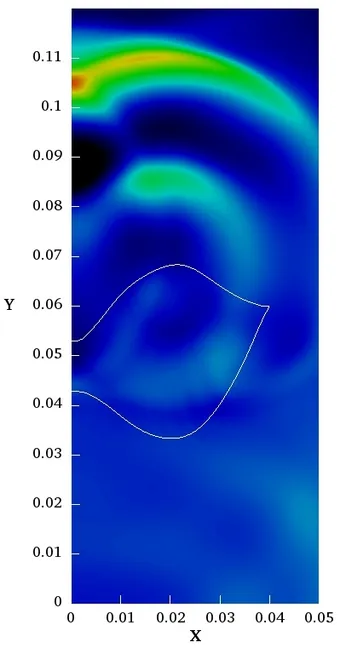
Self-adaptive absorbing boundary conditions
The following pictures show a wave configuration with two sources inside the computational domain. The transparent area around the actual computational domain shows how the wave would propagate in a larger domain (reference solution). To safe computational costs absorbing boundary conditions can be employed at the boundary of the small square to reduce the domain size but at the same time still avoid unwanted reflections from such an artificial domain truncation.


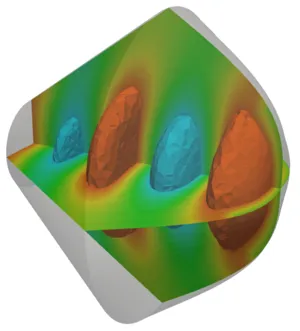
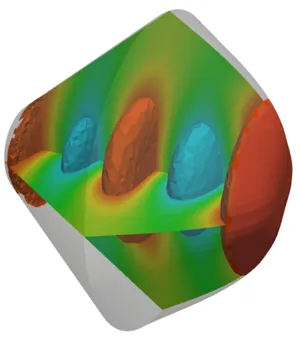
In more than one dimension the angle of incidence of a wave has to be considered to obtain more sophisticated absorbing boundary conditions. This angle can be attained by computing the wave propagation direction for example using the Poynting vector and hence wave-field gradient, which is readily available in the finite element framwork. The next two pictures show the wave propagation field in a 2D and a 3D setting.
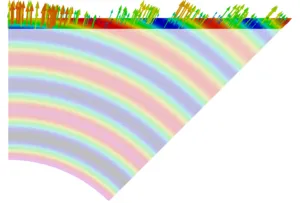

With the angle dependent and self-adapting nonlinear absorbing boundary conditions at work, the wave propagation in a 3D transducer geometry is shown in the following pictures: